
한 상자에 6개의 물건이 들어있다.
그 중 2개가 불량품입니다.
3개를 추출했을 때 적어도 1개의 불량품이 발견될 확률은 ?
어렸을 때 수학 시간에 많이 다루어 보았던 문제입니다.
적어도 1개 확률 = 1 - 모두 아닐 확률
공식으로 구했던 것 같습니다.
다시 알아보도록 하겠습니다.
## 베르누이 / 베르누이 확률 ?
# 베르누이 시행
실험 / 관찰의 결과로 발생 가능한 사상이 단 두가지인 경우
ex) 실패 or 성공 / 정상 or 비정상 / 양품 or 불량품
# 베르누이 시행 조건
1. 시행 결과를 확률변수 X , X = 0 or 1
1은 사상의 성공 , 0은 사상의 실패로 흔히 사용합니다.
2. 각 실험에서 성공할 확률은 p, 실패할 확률은 1-p로 일정합니다.
성공 확률과 실패 확률의 합은 1입니다.
3. 여러 번의 베르누이 시행은 서로 독립입니다.
# 베르누이 확률 분포
성공 1 , 실패 0, 성공 확률 p , 실패 확률 1-p
| X | P(X) |
| 1 | p |
| 0 | 1-p |
P(X)는 probability ,즉 X의 확률입니다.
# 확률의 기대값 , 분산 , 표준편차
1. 기대값 E(X) = 0 x (1-p) + 1 x p = p
2. 분산 var(X) = (0-p)^2(1-p) + (1-p)^(p) = p(1-p)
3. 표준편차 std(X) = var(X)^0.5 = p(1-p)^0.5
## 이항 분포 ?
# 이항 실험
베르누이 시행 조건 외, 동일한 시행을 n번 반복
나타나는 결과의 수에 관심을 가집니다.
즉, 반복적인 베르누이 시행을 이항 실험이라고 합니다.
# 이항 분포
베르누이 시행을 한 번 이상 반복
시행 결과의 합을 변수값으로 하는 확률 변수의 분포 ?
이항 분포
여러 번의 시행 결과가 2가지 경우로만 나타납니다.
성공, 또는 실패 횟수의 합을 이항 확률 변수라고 합니다.
이 변수의 확률 분포를 이항 분포라고 합니다.
성공 확률 p, 반복 횟수 n인 베르누이 시행
X = 성공 횟수, 확률 변수 X는 모수가 (n,p)인 이항분포를 따른다고 한다.
X~B(n,p)로 작성한다.
# 이항 확률 함수
한 시행의 성공 확률 p, 시행을 n회 반복, x는 성공 횟수
성공횟수 X의 확률 함수를 이항 확률 함수라고 합니다.
P(X=x) = nCx * p^x * (1-p)^(n-x)
nCx : n번의 베르누이 시행, 성공 x의 개수를 순서 고려하지 않고 나열하는 방법의 수
# 이항분포 특징 ?
1. 이항분포의 모양은 개별 베르누이 시행에서 성공확률 / 시행 횟수에 따라 결정됩니다.
2. 베르누이 각 시행은 상호 독립적입니다. (별개의 사건)
3. 각각 베르누이 시행에서 성공확률은 모두 동일합니다.
4. 이항분포 확률변수 X는 n개의 독립적인 베르누이 시행의 합 (X=X1+X2+...+Xn)
# 이항 분포 기대값, 분산
1. 기대값 E(X) = p
2. 분산 Var(X) = p(1-p)
# 이항분포 형태
시행횟수 n이 커지면 연속성이 높아집니다.
1. p=0.5 히스토 그램이 좌우 대칭
2. p>0.5 히스토그램 왼쪽 꼬리 분포
3. p<0.5 히스토 그램 오른쪽 꼬리 분포
## 연속성 확인하기
import random
import matplotlib.pyplot as plt
from collections import defaultdict
value=defaultdict(int)
for i in range(1000):
sum=0
for i in range(5):
# 0 or 1랜덤 추출 각 확률 0.5
sum+=random.randint(0,1)
value[sum]+=1
print(value.keys())
print(value.values())
plt.bar(value.keys(),value.values())
조금더 연속성을 가진 그래프 입니다.
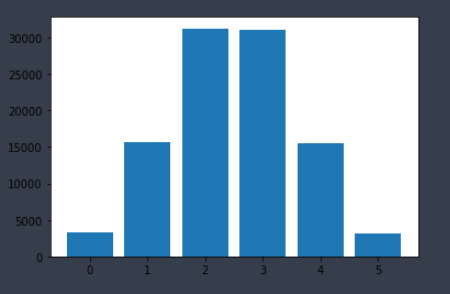
## 꼬리 확인하기
1. 성공 확률을 0.5 이하로 했을 때는 꼬리가 우측으로 생깁니다.
0~1 난수 중 0.75 ~ 1.0 사이인 경우만 1을 더합니다.
즉 0.25의 확률입니다.
2. 성공 확률을 0.5 이상으로 했을 때는 꼬리가 좌측으로 생깁니다.
0~1 난수 중 0.000001 ~ 0.75 사이인 경우에만 1을 더합니다.
즉 0.75의 확률입니다.


그럼 이제 위에서 냈던 문제를 풀어보도록 하겠습니다.
한 상자에 6개의 물건이 들어있다.
그 중 2개가 불량품입니다.
3개를 추출했을 때 적어도 1개의 불량품이 발견될 확률은 ?
양품일 확률(p) : 4/6 = 2/3
불량품일 확률(1-p) : 2/6 = 1/3
n = 3 , x = 3(양품 3개)
이항확률 함수 : P(X=x) = nCx * p^x * (1-p)^(n-x)
P(X=3) = 3C3 * 2/3^3 * 1/3^0
3C3 = 1
2/3 ^3 = 8/27
(1/3)^0 = 1
위 확률은 모두 양품일 확률 ?
확률은 8/27 = 약 0.29입니다.
따라서 1개라도 불량품이 나올 확률은 1-0.29 = 약 0.71 입니다.
## Python 문제 풀기
import random
box=['불','양','불','양','양','양']
value=[1 for i in range(100000) if random.sample(box,3).count('불')!=0]
print(len(value)/100000)
양품 4개 / 불량품 2개 리스트를 생성했습니다.
랜덤으로 3개를 뽑아, 불량품이 1개라도 있다면 1을 리스트에 넣습니다.
위 작업을 10만 번 진행한 후 , 확률을 구했습니다.
왜 0.80이라는 수치가 나왔을까요 ?
이항 분포의 특징 3번
3. 각각 베르누이 시행에서 성공확률은 모두 동일합니다.
하지만 , 위 시행은 비복원 시행입니다.
한 번 뽑은 결과는 다시 박스로 넣지 않습니다.
즉, 첫 확률은 4/6 이었지만 두 번째 확률은 3/5가 됩니다.
마지막 확률은 2/4 입니다.
## SQL 문제 풀어보기
select 1-(4*3*2)/(6*5*4)
from dual;
복원 / 비복원에 따라 결과값이 달라지는 상황 입니다.
분석 하려는 데이터의 특성에 맞게 잘 활용할 수 있도록
여러 수학적 개념을 공부해야 될 것 같습니다!
읽어주셔서 감사합니다,
'알고리즘' 카테고리의 다른 글
| [Python algo] 중앙값 계산 | 중앙값 사용 (0) | 2021.01.20 |
|---|---|
| [Python algo] 탐욕 알고리즘 | Greedy algorithm (7) | 2021.01.19 |
| [Python&SQL] 치환문자를 통해 피타고라스 정리 구현 (1) | 2021.01.18 |
| [Python&SQL] 각 자리수 합 더하기 (2) | 2021.01.15 |
| [Python & SQL] 몬테 카를로 | 원주율 구하기 (1) | 2021.01.09 |
| [Python] 없는 수가 뭘까 ? 빠진수 찾기 (6) | 2021.01.07 |
| [Python] 주사위 던지기 (2) | 2021.01.05 |
| [Python&SQL] 동전의 앞면이 나올 확률은 ? Random (0) | 2021.01.04 |