
안녕하세요.
분산 / 표준편차 값들은 데이터의 퍼짐을 파악하기 위해 필요한 값입니다.
# 분산 ? 표준편차 ?
2021/01/21 - [데이터 분석] - [데이터 분석] 표준편차 | 분산
[데이터 분석] 표준편차 | 분산
안녕하세요 지난 데이터 분석 포스팅 시간에는 대푯값에 대해 공부했습니다. 평균 / 중앙값 / 최빈값 각 의미와 사용시 장단점을 알아보았습니다. # 데이터 탐색 순서 평균값 -> 중앙값 -> 최빈
lsh-story.tistory.com
파이썬에는 분산 , 표준편차를 구하는 다양하고 편한 함수들이 있습니다.
Numpy , pandas , math 등 다양한 모듈을 사용하면
분산과 표준편차를 쉽고 간단하게 구할 수 있습니다.
하지만 직접 분산과 표준편차를 구할 수 있는 코드를 구현하면서
분산과 표준편차를 더 잘 이해할 수 있는 시간을 가져보려고 합니다.
# 분산(Variance) 구하기

분산을 구하는 방법은 각 데이터의 편차 제곱 합을 구하는 것입니다.
따라서 구하는 순서는 다음과 같이 정했습니다.
1. 데이터 평균 구하기
2. 각 데이터 편차 제곱 합 구하기
3. 데이터 개수로 나누기
# 표준편차(standard deviation) 구하기
분산을 먼저 구한 후, 제곱근 사용합니다.
0.5 제곱을 사용하겠습니다
### Python 분산 , 표준편차 구하기
데이터는 emp 테이블의 월급을 사용하겠습니다.
import csv
# 데이터 임포트
f=open('d:\\emp2.csv','r')
emp=csv.reader(f)
# 헤더 삭제 (empno, ename, job ... 등)
next(emp)
# 월급 데이터(index=5) 추출
data=[int(i[5]) for i in emp]
print(data) # 데이터 확인
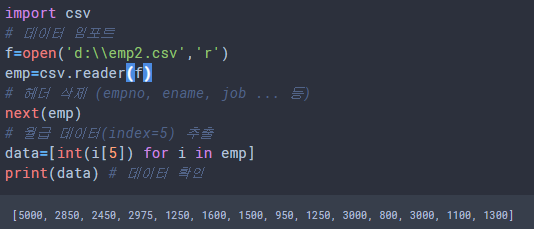
데이터를 임포트하고, 저장한 결과입니다.
# 평균 구하기
m=sum(data)/len(data)
print('평균 : ',m)
# 편차(데이터 - 평균) 제곱 합 담을 변수
ss=0
for i in data:
ss+=pow(i-m,2)
# 분산 : 편차 제곱 합 / 데이터 개수
var=ss/len(data)
print('분산 : ',var)
# 표준편차 : 분산 제곱근
print('표준편차 : ',pow(var,1/2))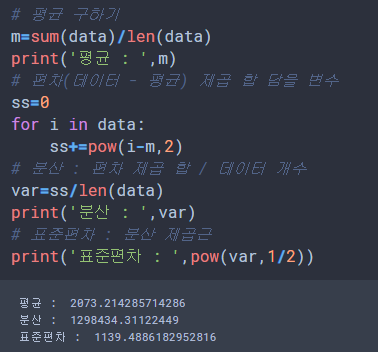
이론으로 배운 것 처럼 분산은 모든 편차의 음수를 없애기 위해 제곱을 했습니다.
그러다보니 값이 상당히 커져있는 것을 확인했습니다.
다시 제곱근을 사용해 표준편차로 만들어서 확인했습니다.
1139라는 수치는 800 ~ 5000 사이에 있는 월급 데이터의 표준 편차로 사용하기 알맞은 수치입니다.
만들어져 있는 함수를 사용하지 않고
직접 분산과 표준편차를 구하며 분산과 표준편차를 더 잘 알게 되었습니다.
이제 편히 만들어져 있는 함수를 사용하고, 언제 사용해야 하는지 잘 알게 되었습니다.
읽어주셔서 감사합니다.
'알고리즘' 카테고리의 다른 글
| [VScode] C++ 환경 설정 (0) | 2023.11.25 |
|---|---|
| [Python algo] 연속 확률 밀도 함수 데이터 생성 및 시각화 (0) | 2021.02.17 |
| [Python algo] 중앙값 계산 | 중앙값 사용 (0) | 2021.01.20 |
| [Python algo] 탐욕 알고리즘 | Greedy algorithm (7) | 2021.01.19 |
| [Python&SQL] 치환문자를 통해 피타고라스 정리 구현 (1) | 2021.01.18 |
| [Python&SQL] 각 자리수 합 더하기 (2) | 2021.01.15 |
| [Python&SQL] 적어도 불량품 1개일 확률 ? (7) | 2021.01.14 |
| [Python & SQL] 몬테 카를로 | 원주율 구하기 (1) | 2021.01.09 |